Мы уже не раз складывали два простых числа, две десятичные дроби или даже простое число с десятичной дробью. Однако мир состоит не только из примитивных данных, порой нам приходится работать и с дробями, с обыкновенными дробями.
Обыкновенные дроби #
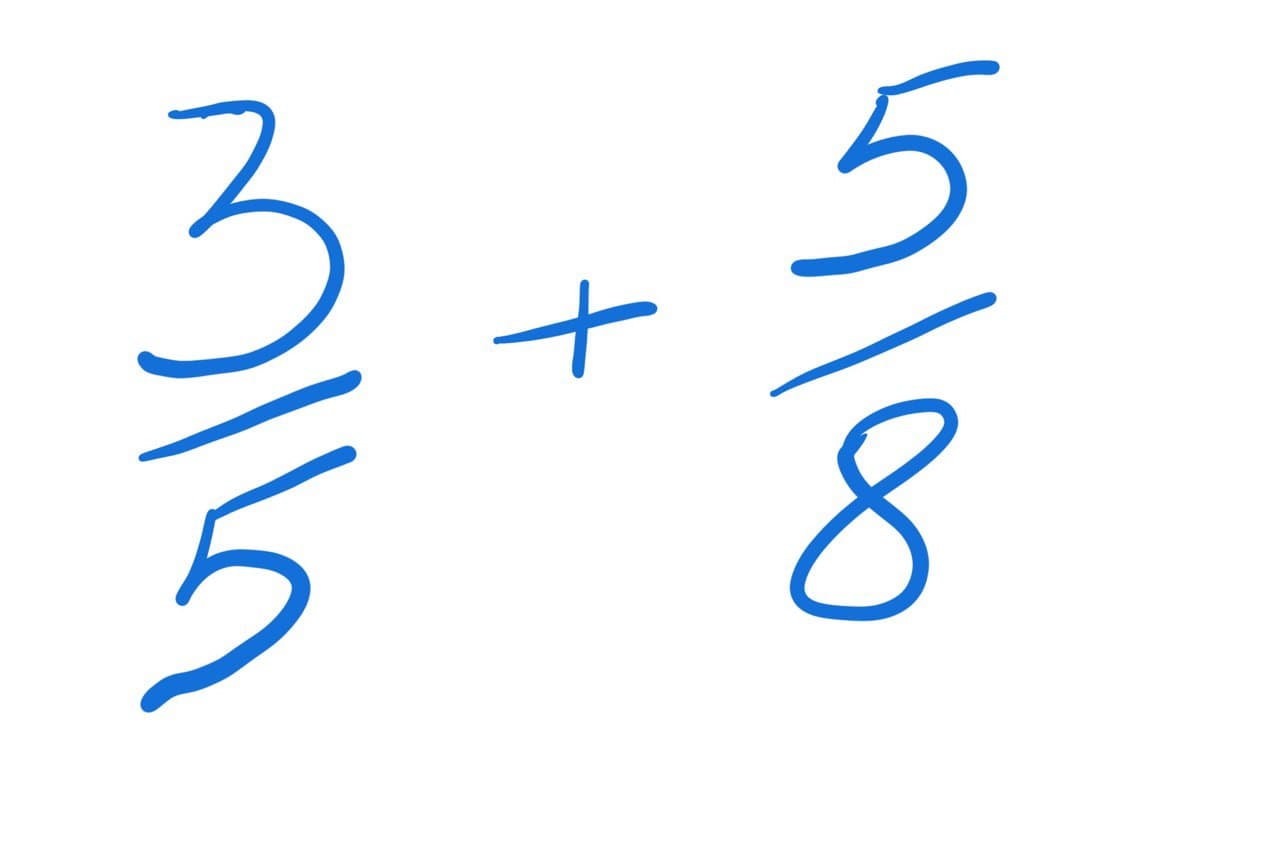
сложение дробей
Обыкновенная дробь, как мы знаем из школы, состоит из двух частей: верхней и нижней. Это если не считать чёрточку посередине за часть дроби. Верхнюю часть дроби в математике принято называть числитель, а нижнюю часть знаменатель. В английском соответственно numerator и denominator.
Для того, что бы мы могли проводить математические операции с дробями мы должны привести их к общему знаменателю и научиться сокращать их. Для этого нам нужно вспомнить про НОД и НОК.
НОД — наибольший общий делитель #
Greatest common divisor — GCD.
НОД´ом для чисел 25 и 15 является 5. Это наибольший общий делитель двух этих чисел. Для чисел 9 и 15 НОД´ом является 3. Оба числа делятся на 3 без остатка. И три является наибольшим общим делителем.
Математика древняя наука и впервые НОД был описан Евклидом в третьем веке до нашей эры. Алгоритм нахождения назван в его честь - Алгори́тм Евкли́да.
В Java Алгоритм Евклида будет реализован вот так:
public static int euclideanAlgorithm(int a, int b) {
while (a != b) {
if (a > b) {
a = a - b;
} else {
b = b - a;
}
}
return a;
}
Этот алгоритм в цикле занимается вычитанием от одной переменной другой и в итоге находит нод. если задуматься, то “бесконечное” вычитание пока A не сравняется с B это деление с нахождением остатка деления. Сегодня у нас есть оператор модуло и мы можем “усовершенствовать” алгоритм:
public static int gcdAlgorithmModulo(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
Этот же алгоритм мы можем решить с применением рекурсии, мы должны прописать условие выхода и само решение:
public static int gcdRecursionAlgorithm(int a, int b) {
if (b == 0) {
return a;
}
return gcdRecursionAlgorithm(b, a % b);
}
Это не единственные способы решения. Всегда ещё можно решить бинарным поиском. Но думаю на этом мы пока уже можем остановиться и сказать, что НОД мы находить научились и можем попробовать найти НОК.
НОК - Наименьшее общее кратное #
Least common multiple — LCM
НОК — это произведение наших двух чисел и делении его на НОД. Реализуется это вот так:
public static int leastCommonMultiple(int a, int b) {
return a / gcdRecursionAlgorithm(a, b) * b;
}
Теперь мы попробуем реализовать правильное “поведение” дробей.
Обыкновенные дроби как объект в Java #
public class Fraction {
private int numerator;
private int denominator;
Fraction(int numerator) {
this.numerator = numerator;
this.denominator = 1;
}
public Fraction(int numerator, int denominator) {
this.numerator = numerator;
this.denominator = denominator;
}
public int getNumerator() {
return numerator;
}
public int getDenominator() {
return denominator;
}
public Fraction sum(Fraction fraction) {
Fraction result = sum(fraction, this);
return result;
}
public static Fraction sum(Fraction a, Fraction b) {
// описать сложение;
// выполнить сокращение дробей, если это возможно
// находим нок знаменателей дробей
// подставить полученное значение в знаменатель РЕЗУЛЬТАТА
// Разделить нок на знаменатели данных дробей.
// умножить числитель и знаменатель каждой дроби на дополнительный множитель
int cDenominator = Math.nok(a.denominator, b.denominator);
int cNumerator =
a.numerator * (cDenominator / a.denominator) +
b.numerator * (cDenominator / b.denominator);
Fraction c = new Fraction(cNumerator, cDenominator);
return c;
}
@Override
public String toString() {
return "Fraction(дробь){" +
"numerator(числитель)=" + numerator +
", denominator(знаменатель)=" + denominator +
'}';
}
}
class Math {
static int nok(int a, int b) {
return a * b / nod(a, b);
}
static int nod(int a, int b) {
if (b == 0) {
return a;
}
return nod(b, a % b);
}
}